In their recent, high-impact, PNAS publications, a Tel Aviv University research group led by Prof. Daphna Joel claims that no difference exists between male and female brain. This was a very high profile study as can be seen by the mentions in The New Scientists, TheGuardian, MedicalPress, IsraelScienceInfo, DailyMail, TheJerusalemPost, CBCNews, and many more.

This publication contradicts much of the corpus of knowledge on brains and gender, and thus took the scientific community by surprise. How can this be?

In short and as put by Carl Sagan: “Absence of evidence is not evidence of absence”.

Indeed, by performing many univariate analyses, the authors show that males and females do not show any particular pattern in the brains’ structure, as least as recorded by MRI scans. It is, however, quite possible for two multivariate data sets to be nicely separated, but not so in any of the “raw” univariate measurements. The following figure is a toy example of a dataset which cannot be separated by any single (raw) variable, but certainly can when considering two variables simultaneously.

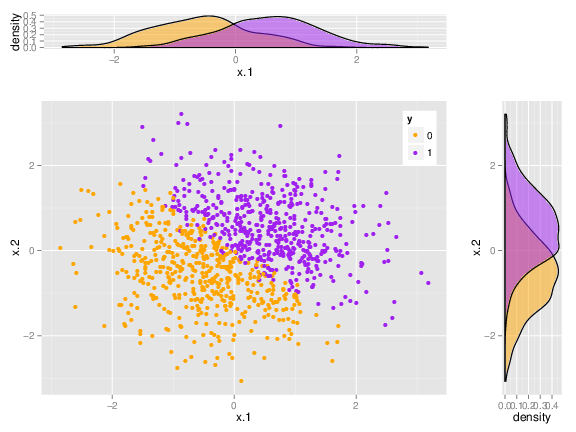
I suspect this is what happened in the case of “Sex Beyond the Genitalia”. When I reanalyzed the same data the multivariate brain structures of males and females was different enough, so that the gender could be inferred from the MRI data alone, with \(~ 80\%\) accuracy(!).

It also seems I was not the only one troubled by Joel et al.’s findings. Here is Del Giudice et al.’s comment, Chekroud et al.’s, Marek Glazerman’s, David Schmidt’s.

In Joel’s reply to the critics they no longer insist that “human brains do not belong to one of two distinct categories: male brain/female brain”, but rather soften their claims: “it is unclear what the biological meaning of the new space is and in what sense brains that seem close in this space are more similar than brains that seem distant”.

I agree. For the purposes of intepreting the dimensions in which male and female differ, some feature selection can be introduced. I will leave that for future neuroimaing research.

Edit(19.3.2016): Here is the code that generated the above figure:

library(mvtnorm)
library(magrittr)
library(MASS)
library(ggplot2)
library(gridExtra)


n <- 1e3
set.seed(999)
X <- rmvnorm(n = n, mean = c(0,0))
beta <- 10*c(1,1)
y <- rbinom(n=n, size = 1, prob=plogis(X %*% beta)) %>% as.factor
xy <- data.frame(x.1=X[,1], x.2=X[,2], y=y)


empty <- ggplot() + geom_point(aes(1, 1), colour = "white") + theme(plot.background = element_blank(), 
    panel.grid.major = element_blank(), panel.grid.minor = element_blank(), 
    panel.border = element_blank(), panel.background = element_blank(), axis.title.x = element_blank(), 
    axis.title.y = element_blank(), axis.text.x = element_blank(), axis.text.y = element_blank(), 
    axis.ticks = element_blank())

# scatterplot of x and y variables
scatter <- ggplot(xy, aes(x.1, x.2)) + geom_point(aes(color = y)) + scale_color_manual(values = c("orange", 
    "purple")) + theme(legend.position = c(1, 1), legend.justification = c(1, 
    1))

# marginal density of x - plot on top
plot_top <- ggplot(xy, aes(x.1, fill = y)) + geom_density(alpha = 0.5) + 
    scale_fill_manual(values = c("orange", "purple")) + theme(legend.position = "none")

# marginal density of y - plot on the right
plot_right <- ggplot(xy, aes(x.2, fill = y)) + geom_density(alpha = 0.5) + 
    coord_flip() + scale_fill_manual(values = c("orange", "purple")) + theme(legend.position = "none")

grid.arrange(plot_top, empty, scatter, plot_right, ncol = 2, nrow = 2, widths = c(4, 
    1), heights = c(1, 4))