Chapter 5 Exploratory Data Analysis

Exploratory Data Analysis (EDA) is a term coined by John W. Tukey in his seminal book (Tukey 1977). It is also (arguably) known as Visual Analytics, or Descriptive Statistics. It is the practice of inspecting, and exploring your data, before stating hypotheses, fitting predictors, and other more ambitious inferential goals. It typically includes the computation of simple summary statistics which capture some property of interest in the data, and visualization. EDA can be thought of as an assumption free, purely algorithmic practice.

In this text we present EDA techniques along the following lines:

  • How we explore: with summary-statistics, or visually?
  • How many variables analyzed simultaneously: univariate, bivariate, or multivariate?
  • What type of variable: categorical or continuous?

5.1 Summary Statistics

5.1.1 Categorical Data

Categorical variables do not admit any mathematical operations on them. We cannot sum them, or even sort them. We can only count them. As such, summaries of categorical variables will always start with the counting of the frequency of each category.

5.1.1.1 Summary of Univariate Categorical Data

# Make some data
gender <- c(rep('Boy', 10), rep('Girl', 12))
drink <- c(rep('Coke', 5), rep('Sprite', 3), rep('Coffee', 6), rep('Tea', 7), rep('Water', 1))  
age <-  sample(c('Young', 'Old'), size = length(gender), replace = TRUE)
# Count frequencies
table(gender)
## gender
##  Boy Girl 
##   10   12
table(drink)
## drink
## Coffee   Coke Sprite    Tea  Water 
##      6      5      3      7      1
table(age)
## age
##   Old Young 
##    12    10

If instead of the level counts you want the proportions, you can use prop.table

prop.table(table(gender))
## gender
##       Boy      Girl 
## 0.4545455 0.5454545

5.1.1.2 Summary of Bivariate Categorical Data

library(magrittr)
cbind(gender, drink) %>% head # bind vectors into matrix and inspect (`c` for column)
##      gender drink   
## [1,] "Boy"  "Coke"  
## [2,] "Boy"  "Coke"  
## [3,] "Boy"  "Coke"  
## [4,] "Boy"  "Coke"  
## [5,] "Boy"  "Coke"  
## [6,] "Boy"  "Sprite"
table1 <- table(gender, drink) # count frequencies of bivariate combinations
table1                                      
##       drink
## gender Coffee Coke Sprite Tea Water
##   Boy       2    5      3   0     0
##   Girl      4    0      0   7     1

5.1.1.3 Summary of Multivariate Categorical Data

You may be wondering how does R handle tables with more than two dimensions. It is indeed not trivial to report this in a human-readable way. R offers several solutions: table is easier to compute with, and ftable is human readable.

table2.1 <- table(gender, drink, age) # A machine readable table. 
table2.1
## , , age = Old
## 
##       drink
## gender Coffee Coke Sprite Tea Water
##   Boy       2    1      1   0     0
##   Girl      3    0      0   5     0
## 
## , , age = Young
## 
##       drink
## gender Coffee Coke Sprite Tea Water
##   Boy       0    4      2   0     0
##   Girl      1    0      0   2     1
table.2.2 <- ftable(gender, drink, age) # A human readable table (`f` for Flat).
table.2.2
##               age Old Young
## gender drink               
## Boy    Coffee       2     0
##        Coke         1     4
##        Sprite       1     2
##        Tea          0     0
##        Water        0     0
## Girl   Coffee       3     1
##        Coke         0     0
##        Sprite       0     0
##        Tea          5     2
##        Water        0     1

If you want proportions instead of counts, you need to specify the denominator, i.e., the margins. Think: what is the margin in each of the following outputs?

prop.table(table1, margin = 1) # every *row* sums to to 1
##       drink
## gender     Coffee       Coke     Sprite        Tea      Water
##   Boy  0.20000000 0.50000000 0.30000000 0.00000000 0.00000000
##   Girl 0.33333333 0.00000000 0.00000000 0.58333333 0.08333333
prop.table(table1, margin = 2) # every *column* sums to 1
##       drink
## gender    Coffee      Coke    Sprite       Tea     Water
##   Boy  0.3333333 1.0000000 1.0000000 0.0000000 0.0000000
##   Girl 0.6666667 0.0000000 0.0000000 1.0000000 1.0000000

5.1.2 Continous Data

Continuous variables admit many more operations than categorical. We can compute sums, means, quantiles, and more.

5.1.2.1 Summary of Univariate Continuous Data

We distinguish between several types of summaries, each capturing a different property of the data.

5.1.2.2 Summary of Location

Capture the “location” of the data. These include:

Definition 5.1 (Average) The mean, or average, of a sample \(x:=(x_1,\dots,x_n)\), denoted \(\bar x\) is defined as \[ \bar x := n^{-1} \sum x_i. \]

The sample mean is non robust. A single large observation may inflate the mean indefinitely. For this reason, we define several other summaries of location, which are more robust, i.e., less affected by “contaminations” of the data.

We start by defining the sample quantiles, themselves not a summary of location.

Definition 5.2 (Quantiles) The \(\alpha\) quantile of a sample \(x\), denoted \(x_\alpha\), is (non uniquely) defined as a value above \(100 \alpha \%\) of the sample, and below \(100 (1-\alpha) \%\).

We emphasize that sample quantiles are non-uniquely defined. See ?quantile for the 9(!) different definitions that R provides.

Using the sample quantiles, we can now define another summary of location, the median.

Definition 5.3 (Median) The median of a sample \(x\), denoted \(x_{0.5}\) is the \(\alpha=0.5\) quantile of the sample.

A whole family of summaries of locations is the alpha trimmed mean.

Definition 5.4 (Alpha Trimmed Mean) The \(\alpha\) trimmed mean of a sample \(x\), denoted \(\bar x_\alpha\) is the average of the sample after removing the \(\alpha\) proportion of largest and \(\alpha\) proportion of smallest observations.

The simple mean and median are instances of the alpha trimmed mean: \(\bar x_0\) and \(\bar x_{0.5}\) respectively.

Here are the R implementations:

x <- rexp(100) # generate some (assymetric) random data
mean(x) # simple mean
## [1] 1.017118
median(x) # median
## [1] 0.5805804
mean(x, trim = 0.2) # alpha trimmed mean with alpha=0.2
## [1] 0.7711528

5.1.2.3 Summary of Scale

The scale of the data, sometimes known as spread, can be thought of its variability.

Definition 5.5 (Standard Deviation) The standard deviation of a sample \(x\), denoted \(S(x)\), is defined as \[ S(x):=\sqrt{(n-1)^{-1} \sum (x_i-\bar x)^2} . \]

For reasons of robustness, we define other, more robust, measures of scale.

Definition 5.6 (MAD) The Median Absolute Deviation from the median, denoted as \(MAD(x)\), is defined as \[MAD(x):= c \: |x-x_{0.5}|_{0.5} . \]

where \(c\) is some constant, typically set to \(c=1.4826\) so that MAD and \(S(x)\) have the same large sample limit.

Definition 5.7 (IQR) The Inter Quartile Range of a sample \(x\), denoted as \(IQR(x)\), is defined as \[ IQR(x):= x_{0.75}-x_{0.25} .\]

Here are the R implementations

sd(x) # standard deviation
## [1] 0.9981981
mad(x) # MAD
## [1] 0.6835045
IQR(x) # IQR
## [1] 1.337731

5.1.2.4 Summary of Asymmetry

Summaries of asymmetry, also known as skewness, quantify the departure of the \(x\) from a symmetric sample.

Definition 5.8 (Yule) The Yule measure of assymetry, denoted \(Yule(x)\) is defined as \[Yule(x) := \frac{1/2 \: (x_{0.75}+x_{0.25}) - x_{0.5} }{1/2 \: IQR(x)} .\]

Here is an R implementation

yule <- function(x){
  numerator <- 0.5 * (quantile(x,0.75) + quantile(x,0.25))-median(x) 
  denominator <- 0.5* IQR(x)
  c(numerator/denominator, use.names=FALSE)
}
yule(x)
## [1] 0.5755205

Things to note:

  • A perfectly symmetric vector will return 0 because the median will be exactly on the midway.
  • It is bounded between -1 and 1 because of the denominator

5.1.2.5 Summary of Bivariate Continuous Data

When dealing with bivariate, or multivariate data, we can obviously compute univariate summaries for each variable separately. This is not the topic of this section, in which we want to summarize the association between the variables, and not within them.

Definition 5.9 (Covariance) The covariance between two samples, \(x\) and \(y\), of same length \(n\), is defined as \[Cov(x,y):= (n-1)^{-1} \sum (x_i-\bar x)(y_i-\bar y) \]

We emphasize this is not the covariance you learned about in probability classes, since it is not the covariance between two random variables but rather, between two samples. For this reasons, some authors call it the empirical covariance, or sample covariance.

Definition 5.10 (Pearson’s Correlation Coefficient) Peasrson’s correlation coefficient, a.k.a. Pearson’s moment product correlation, or simply, the correlation, denoted r(x,y), is defined as \[r(x,y):=\frac{Cov(x,y)}{S(x)S(y)}. \]

If you find this definition enigmatic, just think of the correlation as the covariance between \(x\) and \(y\) after transforming each to the unitless scale of z-scores.

Definition 5.11 (Z-Score) The z-scores of a sample \(x\) are defined as the mean-centered, scale normalized observations: \[z_i(x):= \frac{x_i-\bar x}{S(x)}.\]

We thus have that \(r(x,y)=Cov(z(x),z(y))\).

Here are the R implementations

y <- rexp(100) # generate another vector of some random data
cov(x,y) # covariance between x and y
## [1] -0.03381266
cor(x,y) # correlation between x and y (default is pearson)
## [1] -0.03641364
scale(x) %>% head # z-score of x
##             [,1]
## [1,]  1.72293613
## [2,]  0.83367533
## [3,]  0.27703737
## [4,] -1.00110536
## [5,]  0.07671776
## [6,] -0.66044228

5.1.2.6 Summary of Multivariate Continuous Data

The covariance is a simple summary of association between two variables, but it certainly may not capture the whole “story” when dealing with more than two variables. The most common summary of multivariate relation, is the covariance matrix, but we warn that only the simplest multivariate relations are fully summarized by this matrix.

Definition 5.12 (Sample Covariance Matrix) Given \(n\) observations on \(p\) variables, denote \(x_{i,j}\) the \(i\)’th observation of the \(j\)’th variable. The sample covariance matrix, denoted \(\hat \Sigma\) is defined as \[\hat \Sigma_{k,l}=(n-1)^{-1} \sum_i [(x_{i,k}-\bar x_k)(x_{i,l}-\bar x_l)],\] where \(\bar x_k:=n^{-1} \sum_i x_{i,k}\). Put differently, the \(k,l\)’th entry in \(\hat \Sigma\) is the sample covariance between variables \(k\) and \(l\).
Remark. \(\hat \Sigma\) is clearly non robust. How would you define a robust covariance matrix?

5.2 Visualization

Summarizing the information in a variable to a single number clearly conceals much of the story in the sample. This is like inspecting a person using a caricature, instead of a picture. Visualizing the data, when possible, is more informative.

5.2.1 Categorical Data

Recalling that with categorical variables we can only count the frequency of each level, the plotting of such variables are typically variations on the bar plot.

5.2.1.1 Visualizing Univariate Categorical Data

barplot(table(age))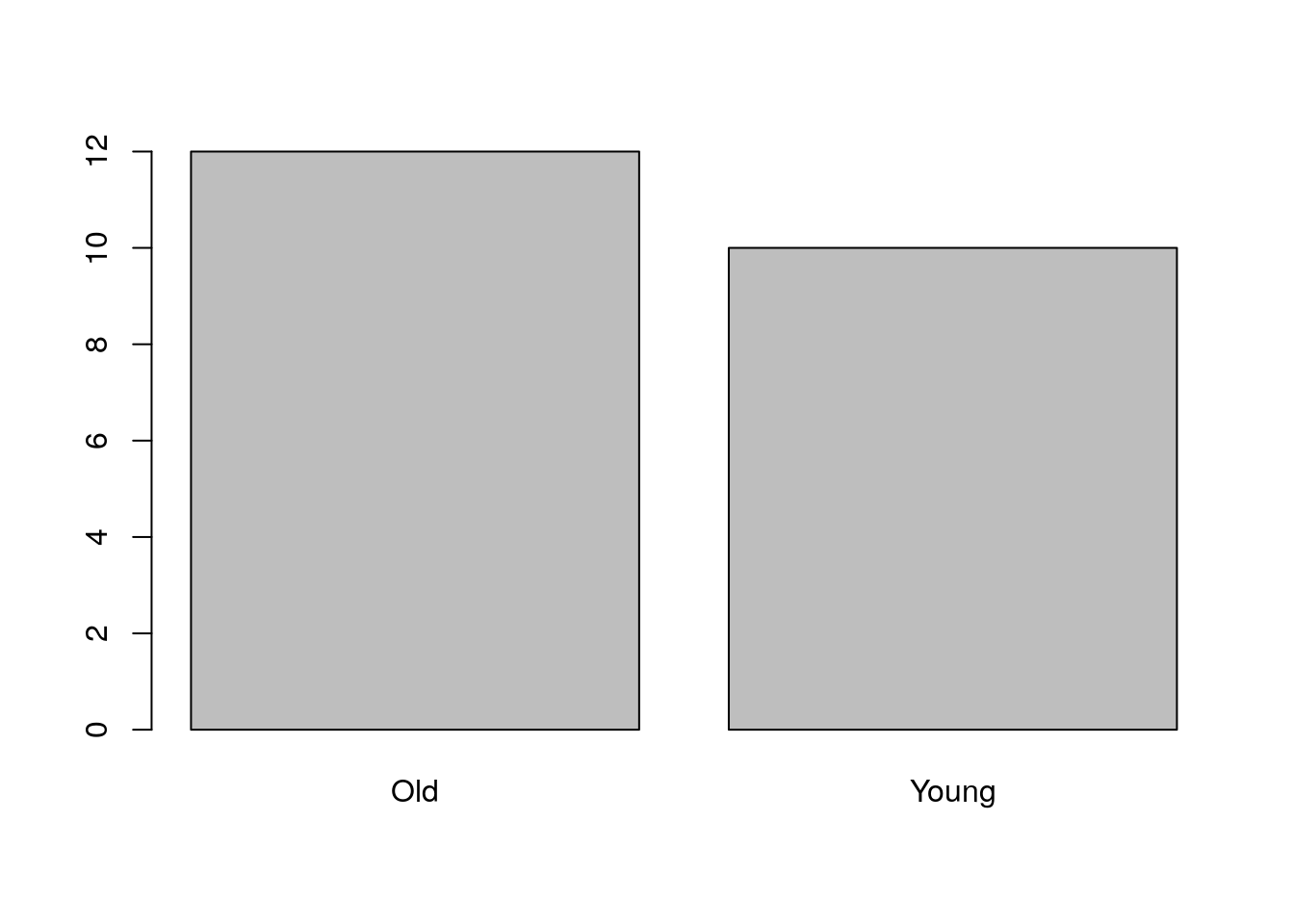

5.2.1.2 Visualizing Bivariate Categorical Data

There are several generalizations of the barplot, aimed to deal with the visualization of bivariate categorical data. They are sometimes known as the clustered bar plot and the stacked bar plot. In this text, we advocate the use of the mosaic plot which is also the default in R.

plot(table1, main='Bivariate mosaic plot')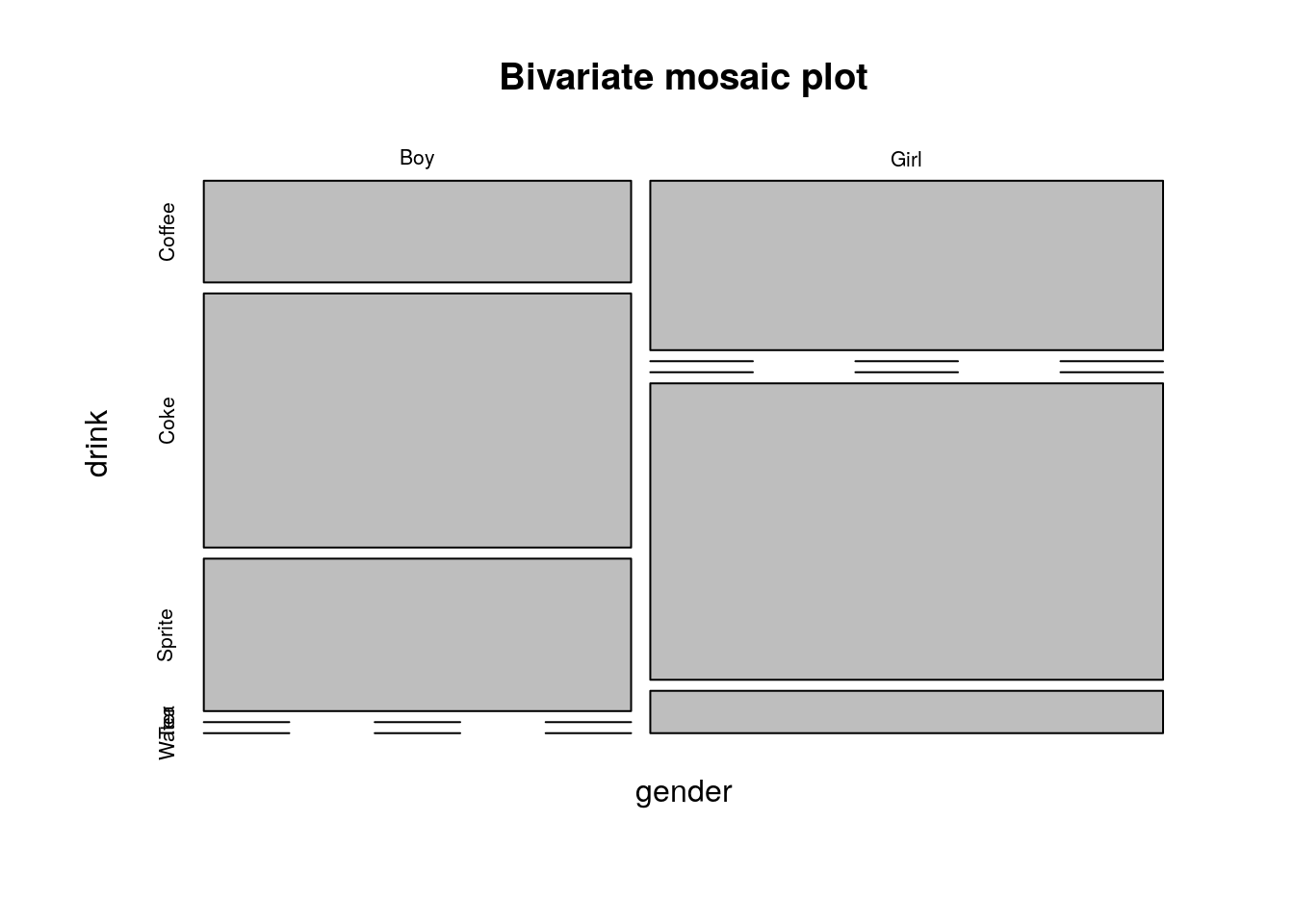

Things to note:

  • The proportion of each category is encoded in the width of the bars (more girls than boys here)
  • Zero observations are marked as a line.

5.2.1.3 Visualizing Multivariate Categorical Data

The mosaic plot is not easy to generalize to more than two variables, but it is still possible (at the cost of interpretability).

plot(table2.1, main='Trivaraite mosaic plot')

When one of the variables is a (discrete) time variable, then the plot has a notion dynamics in time. For this see the Alluvial plot 5.3.1.

If the variables represent a hierarchy, consider a Sunburst Plot:

library(sunburstR)
# read in sample visit-sequences.csv data provided in source
# https://gist.github.com/kerryrodden/7090426#file-visit-sequences-csv
sequences <- read.csv(
  system.file("examples/visit-sequences.csv",package="sunburstR")
  ,header=F
  ,stringsAsFactors = FALSE
)
sunburst(sequences) # In the HTML version of the book this plot is interactive.
Legend

5.2.2 Continuous Data

5.2.2.1 Visualizing Univariate Continuous Data

Unlike categorical variables, there are endlessly many ways to visualize continuous variables. The simplest way is to look at the raw data via the stripchart.

sample1 <- rexp(10)                             
stripchart(sample1)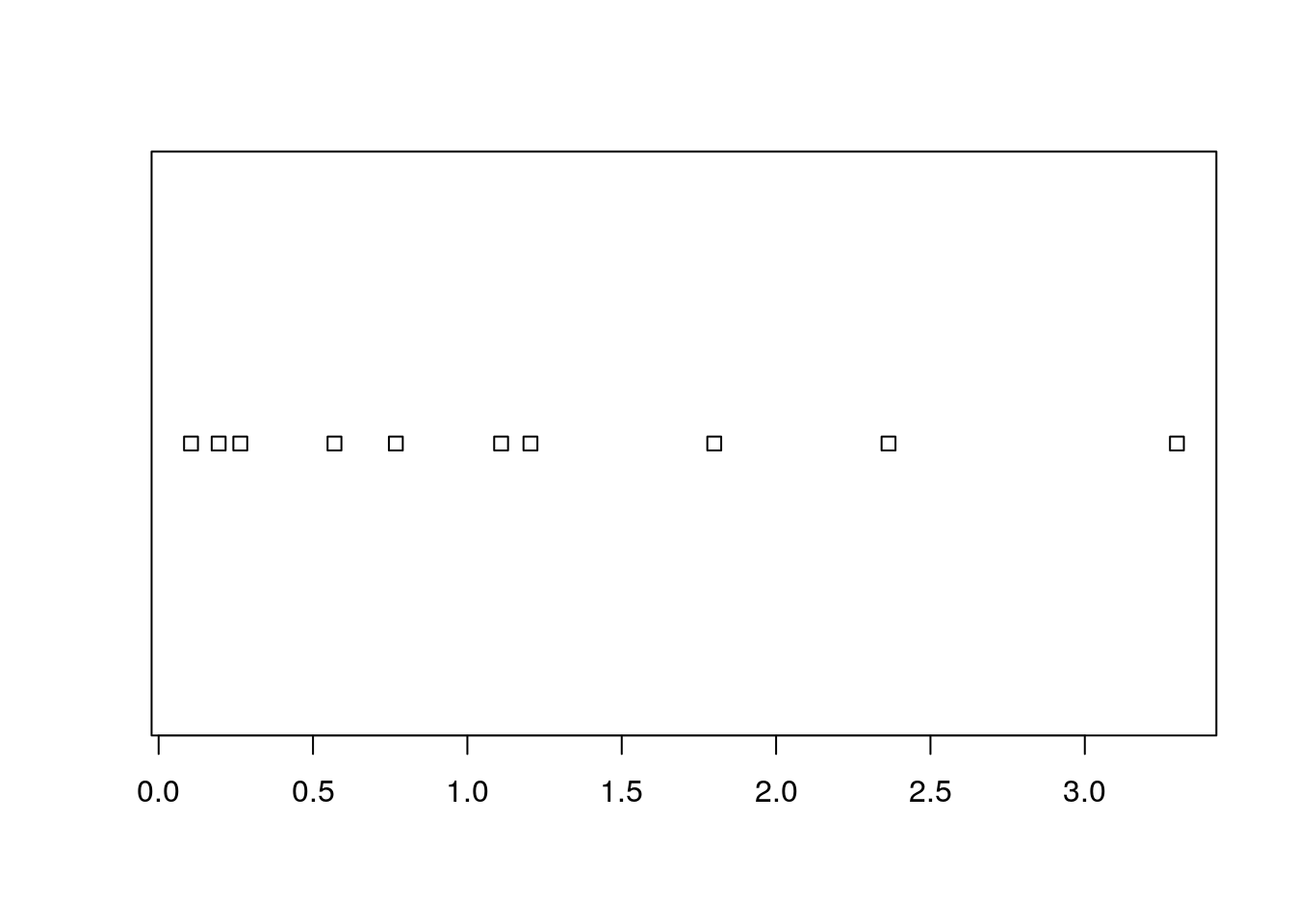

Clearly, if there are many observations, the stripchart will be a useless line of black dots. We thus bin them together, and look at the frequency of each bin; this is the histogram. R’s histogram function has very good defaults to choose the number of bins. Here is a histogram showing the counts of each bin.

sample1 <- rexp(100)                            
hist(sample1, freq=T, main='Counts')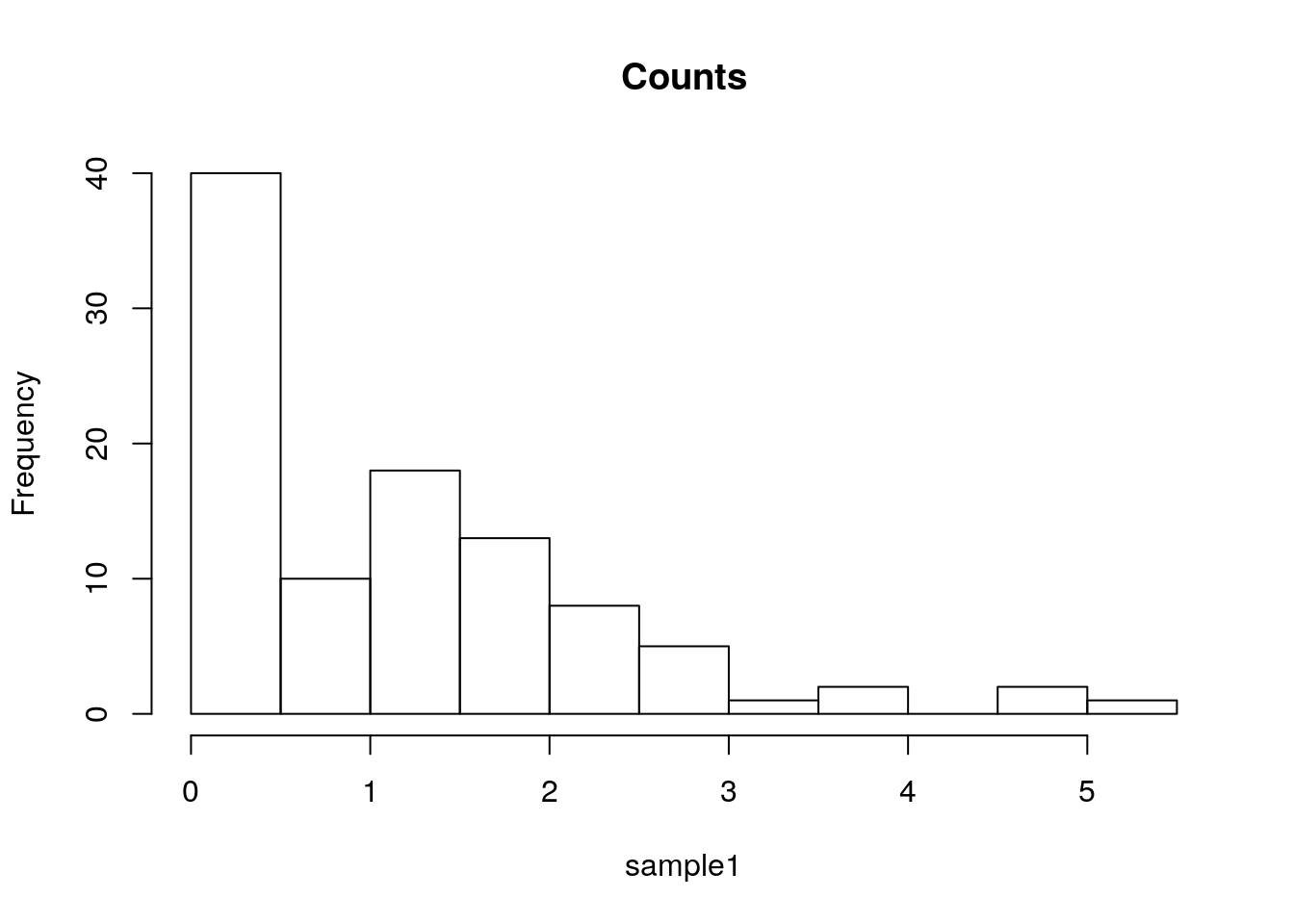

The bin counts can be replaced with the proportion of each bin using the freq argument.

hist(sample1, freq=F, main='Proportion')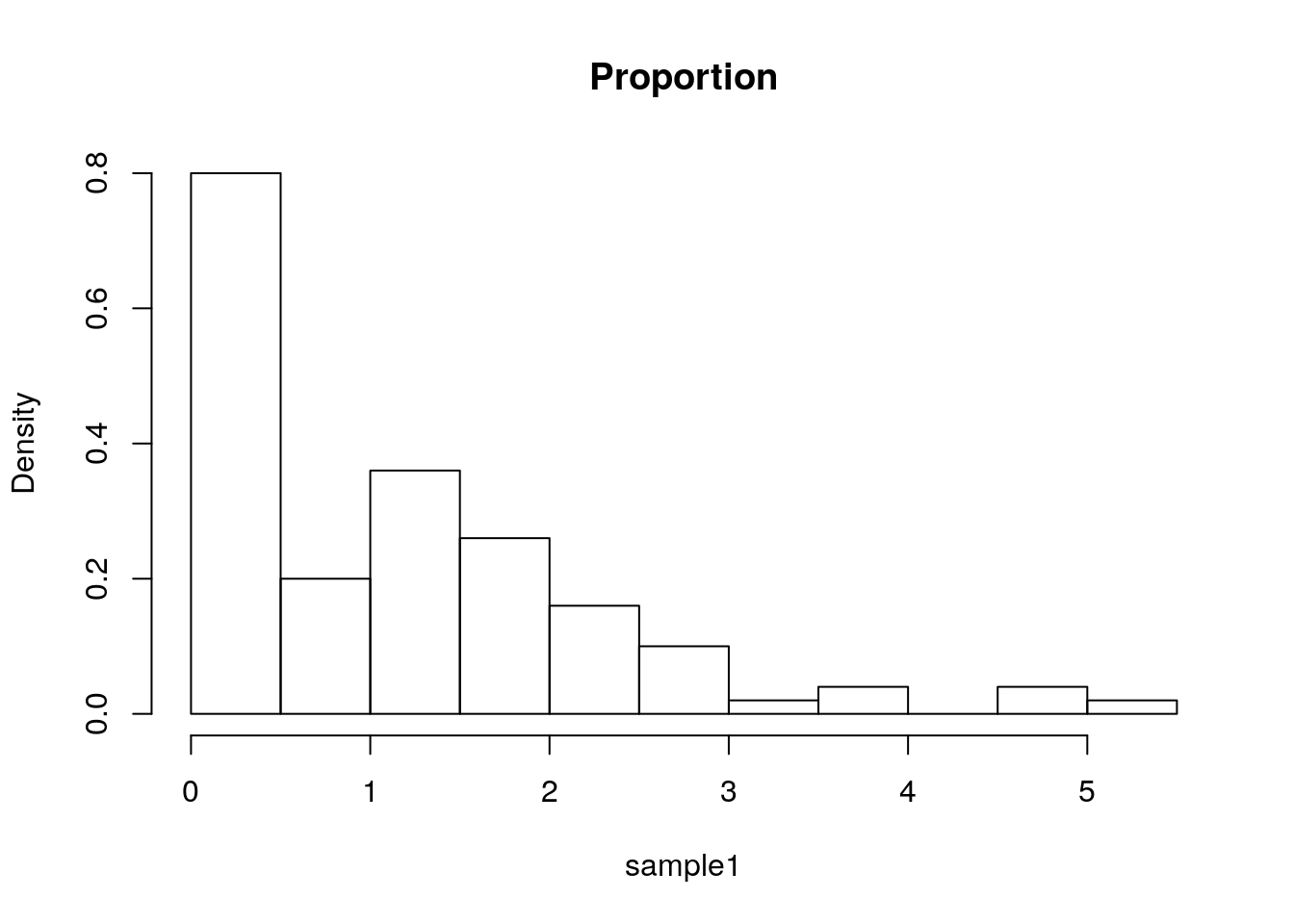

Things to note:

  • The bins’ proportion summary is larger than 1 because it considers each bin’s width, which in this case has a constant width of 0.5, hence the total proportion sum is 1/0.5=2.

The bins of a histogram are non overlapping. We can adopt a sliding window approach, instead of binning. This is the density plot which is produced with the density function, and added to an existing plot with the lines function. The rug function adds the original data points as ticks on the axes, and is strongly recommended to detect artifacts introduced by the binning of the histogram, or the smoothing of the density plot.

hist(sample1, freq=F, main='Frequencies')   
lines(density(sample1))                     
rug(sample1)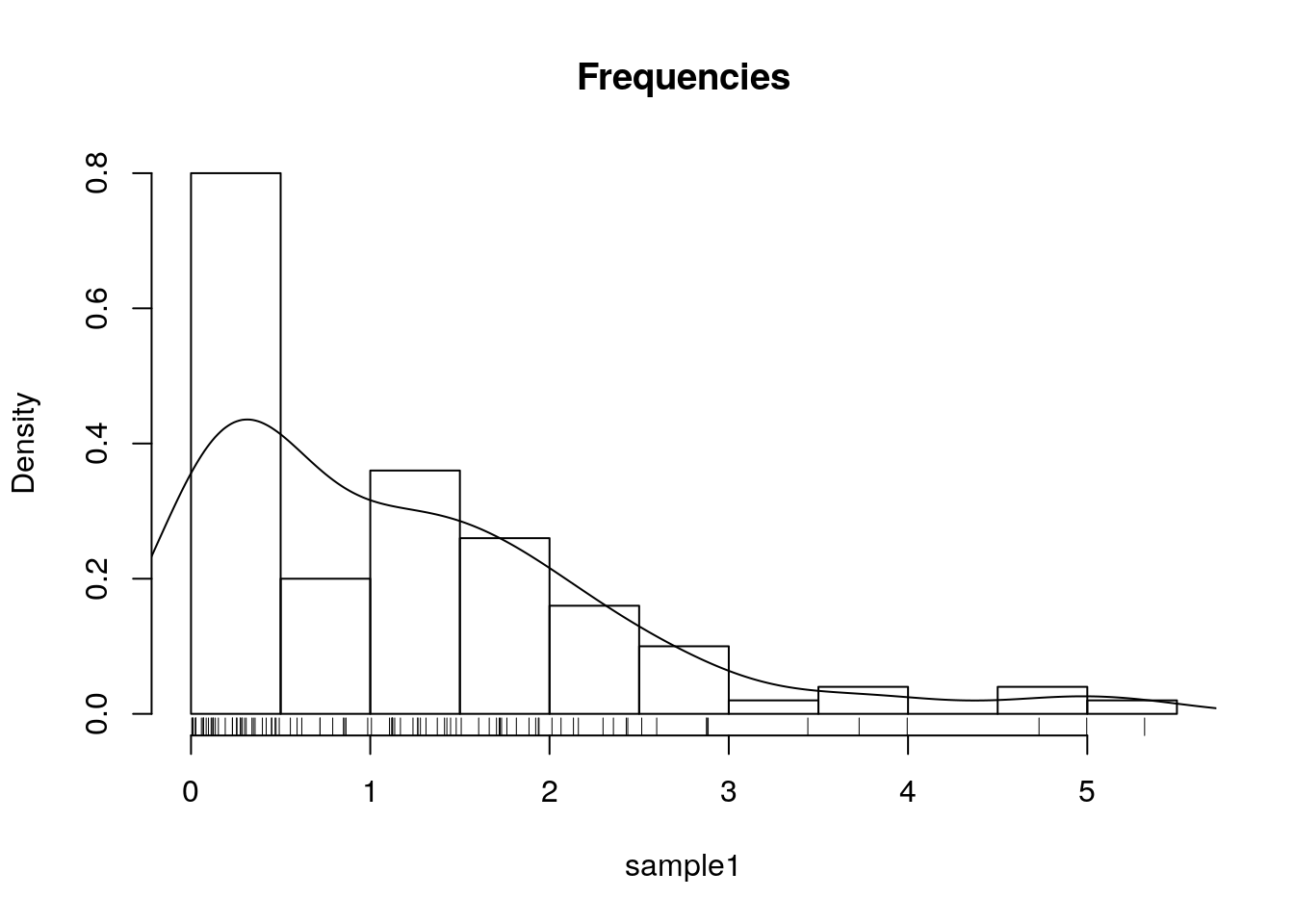

Remark. Why would it make no sense to make a table, or a barplot, of continuous data?

One particularly useful visualization, due to John W. Tukey, is the boxplot. The boxplot is designed to capture the main phenomena in the data, and simultaneously point to outlines.

boxplot(sample1)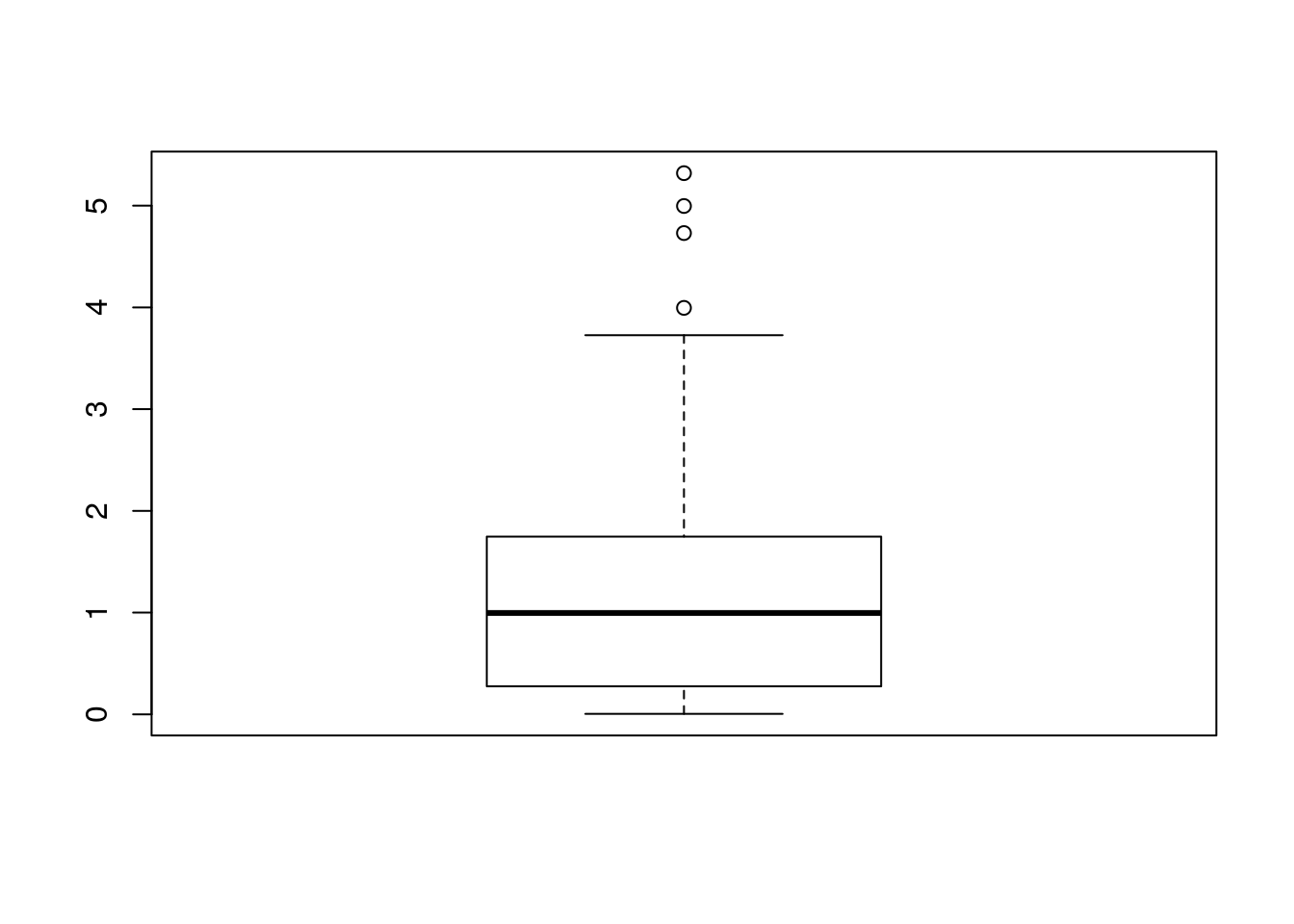

Another way to deal with a massive amount of data points, is to emphasize important points, and conceal non-important. This is the purpose of circle-packing (example from r-graph gallery):

5.2.2.2 Visualizing Bivariate Continuous Data

The bivariate counterpart of the stipchart is the celebrated scatter plot.

n <- 20
x1 <- rexp(n)
x2 <- 2* x1 + 4 + rexp(n)
plot(x2~x1)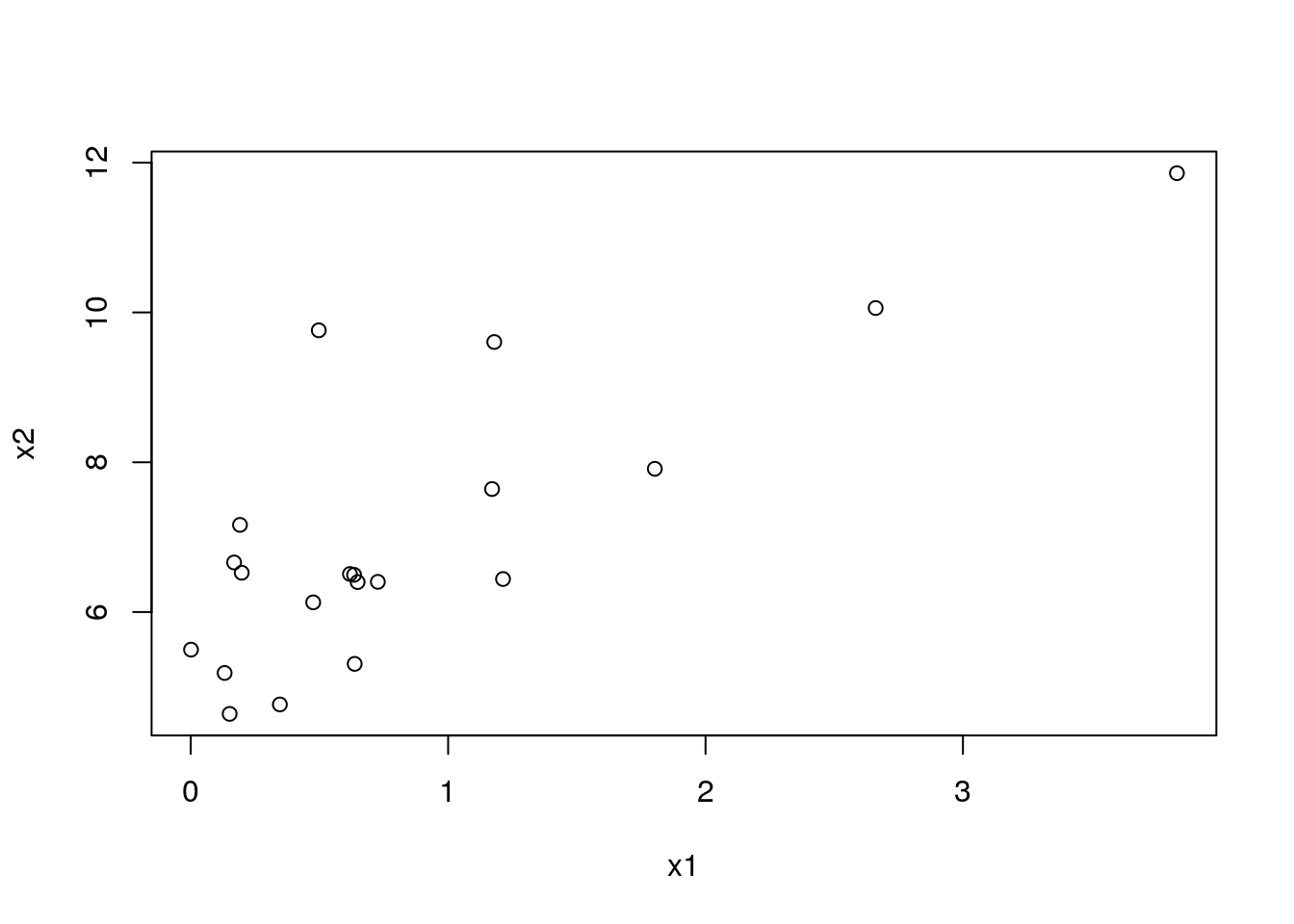

A scatter-plot may be augmented with marginal univariate visualization. See, for instance, the rug function to add the raw data on the margins:

plot(x2~x1)
rug(x1,side = 1)
rug(x2,side = 2)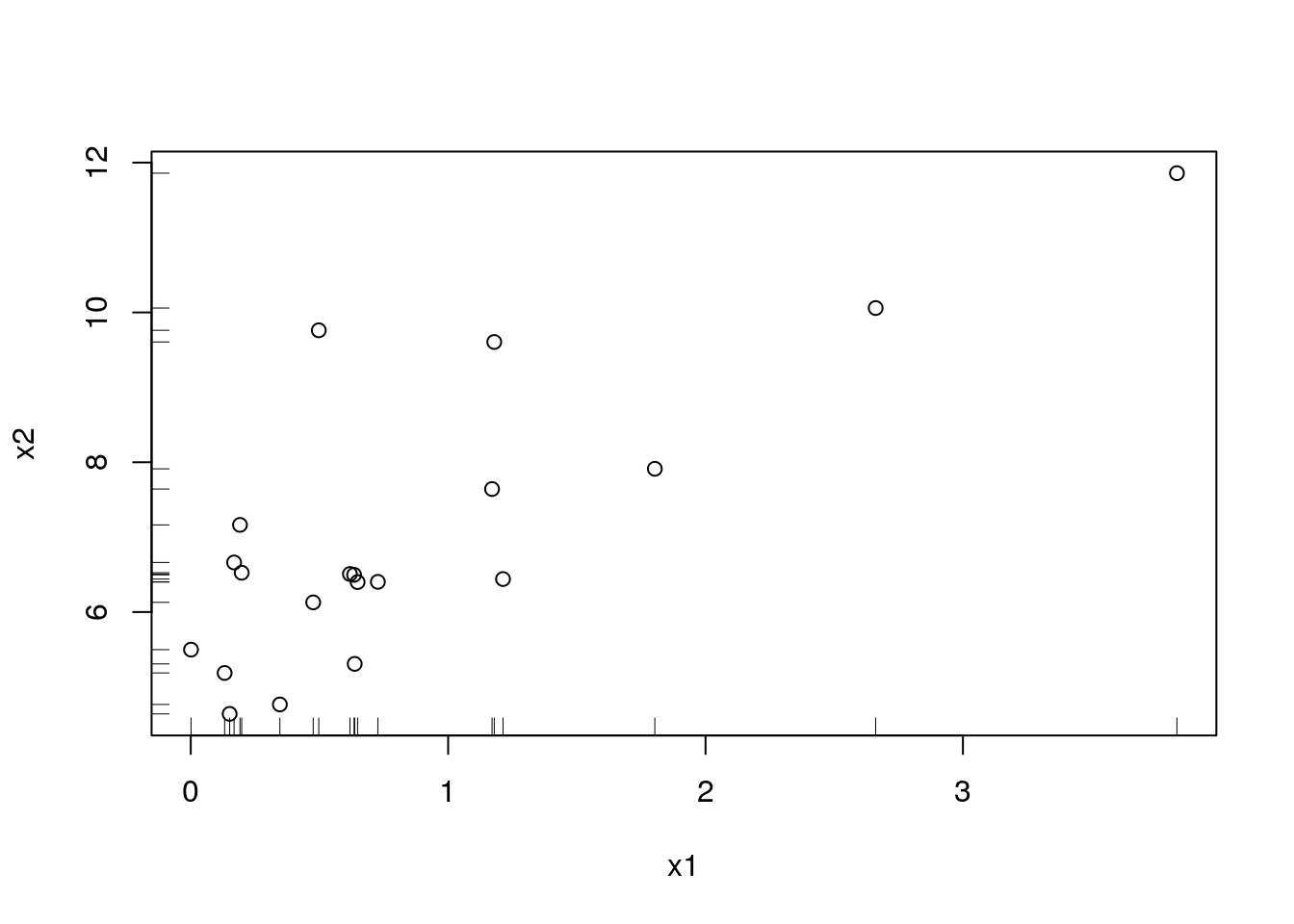

A fancier version may use a histogram on the margins:

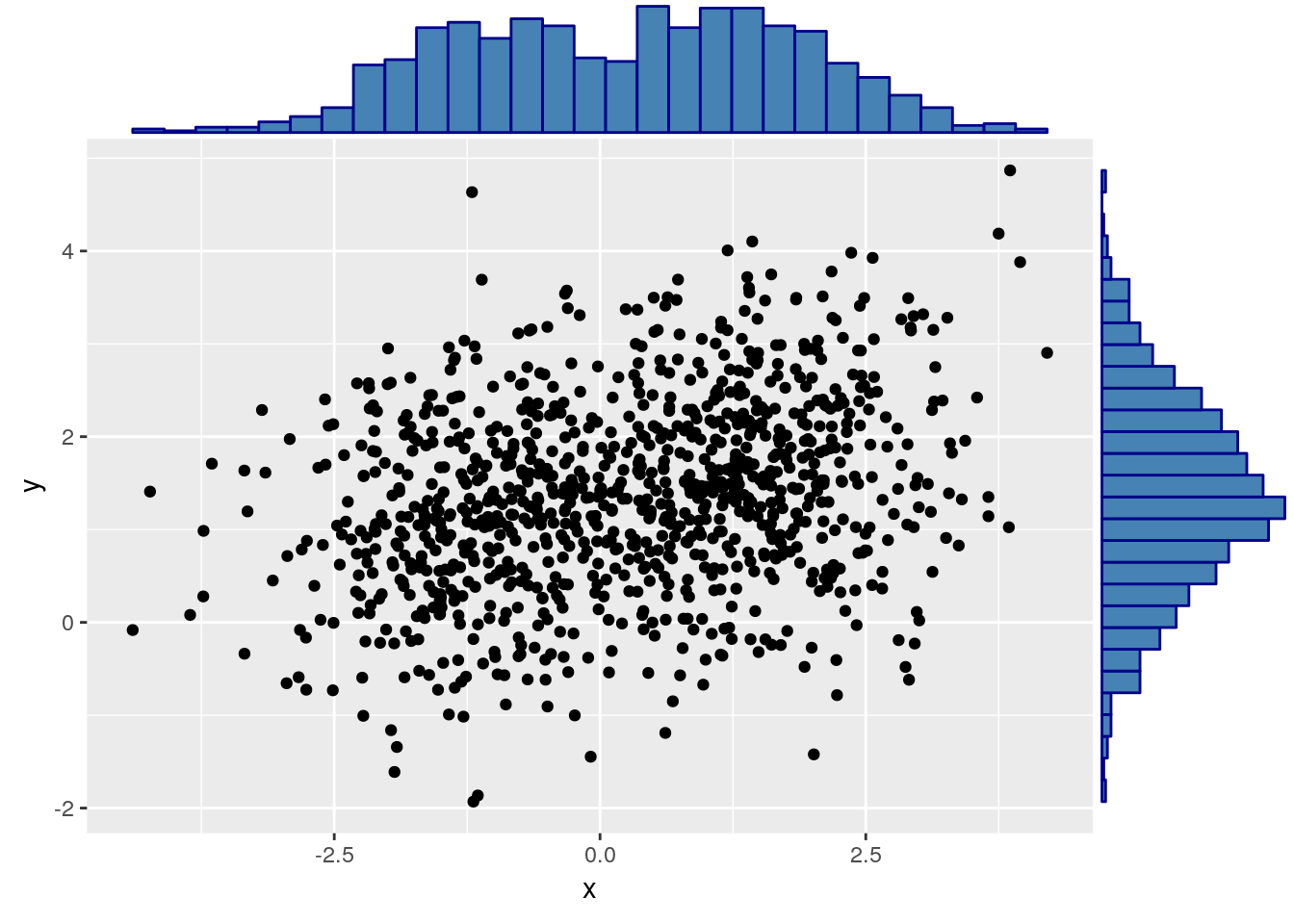
Like the univariate stripchart, the scatter plot will be an uninformative mess in the presence of a lot of data. A nice bivariate counterpart of the univariate histogram is the hexbin plot, which tessellates the plane with hexagons, and reports their frequencies.

library(hexbin) # load required library
n <- 2e5
x1 <- rexp(n)
x2 <- 2* x1 + 4 + rnorm(n)
plot(hexbin(x = x1, y = x2))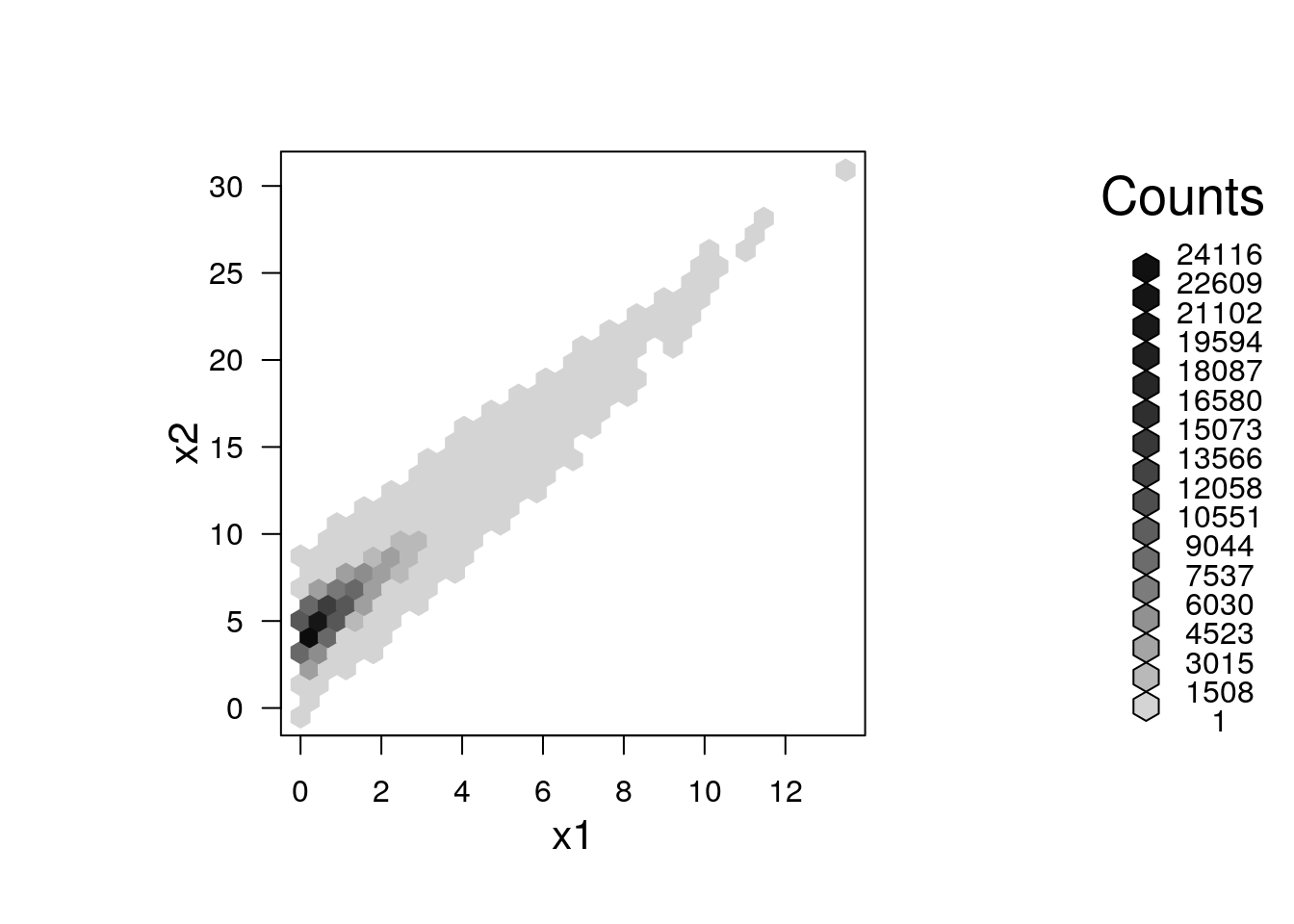

5.2.2.3 Visualizing Multivariate Continuous Data

Visualizing multivariate data is a tremendous challenge given that we cannot grasp \(4\) dimensional spaces, nor can the computer screen present more than \(2\) dimensional spaces. We thus have several options: (i) To project the data to 2D. This is discussed in the Dimensionality Reduction Section 11.1. (ii) To visualize not the raw data, but rather its summaries, like the covariance matrix.

Our own Multinav package adopts an interactive approach. For each (multivariate) observation a simple univariate summary may be computed and visualized. These summaries may be compared, and the original (multivariate) observation inspected upon demand. Contact Efrat for more details.
The Multinav Package

An alternative approach starts with the covariance matrix, \(\hat \Sigma\), that can be visualized as an image. Note the use of the :: operator (called Double Colon Operator, for help: ?'::'), which is used to call a function from some package, without loading the whole package. We will use the :: operator when we want to emphasize the package of origin of a function.

covariance <- cov(longley) # The covariance of the longley dataset
correlations <- cor(longley) # The correlations of the longley dataset
lattice::levelplot(correlations)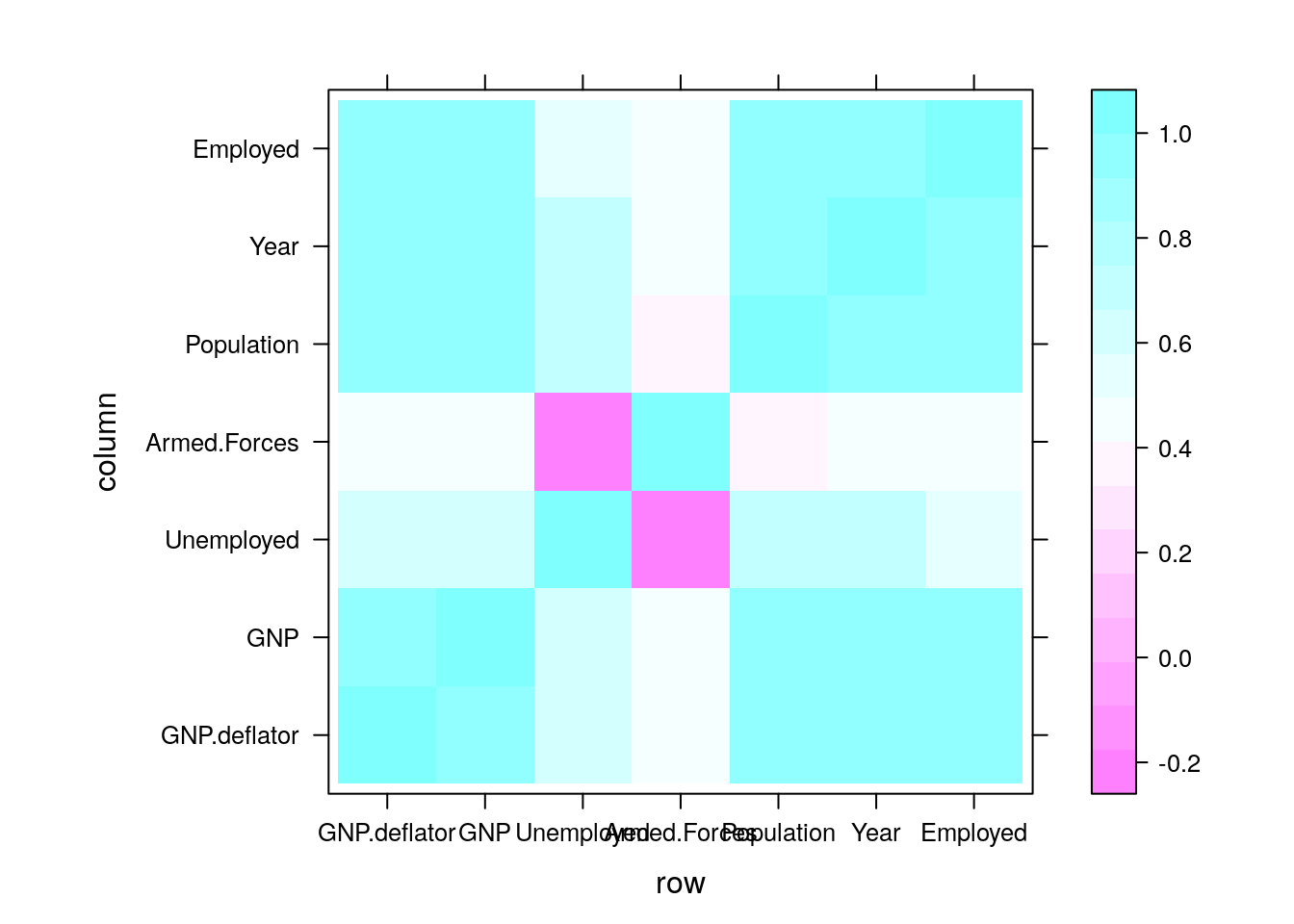

If we believe the covariance has some structure, we can do better than viewing the raw correlations. In temporal, and spatial data, we believe correlations decay as some function of distances. We can thus view correlations as a function of the distance between observations. This is known as a variogram. Note that for a variogram to be informative, it is implied that correlations are merely a function of distances (and not locations themselves). This is formally known as stationary and isotropic correlations.

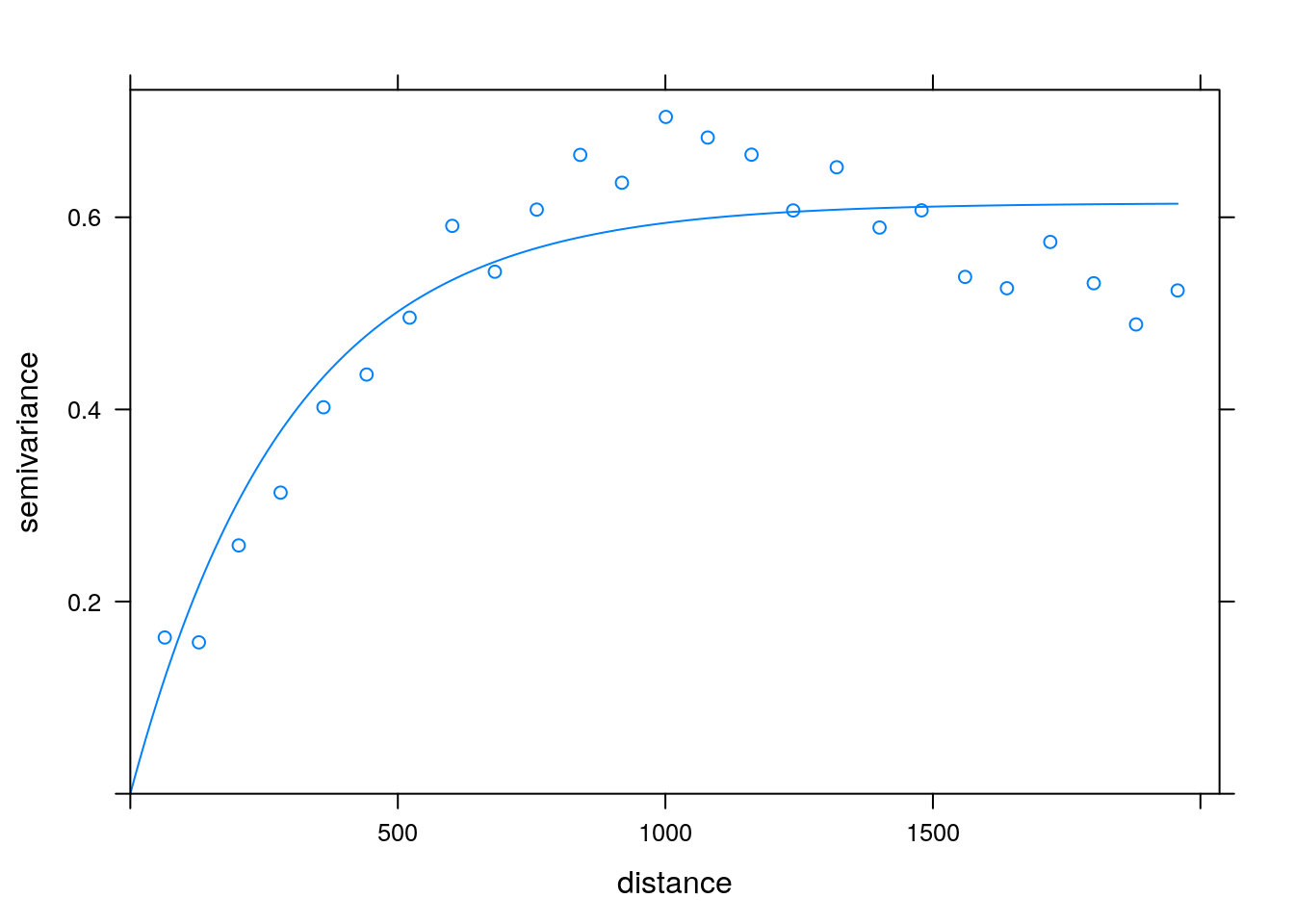
Variogram: plotting correlation as a function of spatial distance. Courtesy of Ron Sarafian.

Variogram: plotting correlation as a function of spatial distance. Courtesy of Ron Sarafian.

5.2.2.4 Parallel Coordinate Plots

In a parallel coordinate plot, we plot a multivariate observation as a function of its coordinates. In the following example, we visualize the celebrated Iris dataset. In this dataset, for each of 50 iris flowers, Edgar Anderson measured 4 characteristics.

ir <- rbind(iris3[,,1], iris3[,,2], iris3[,,3])
MASS::parcoord(log(ir)[, c(3, 4, 2, 1)], col = 1 + (0:149)%/%50)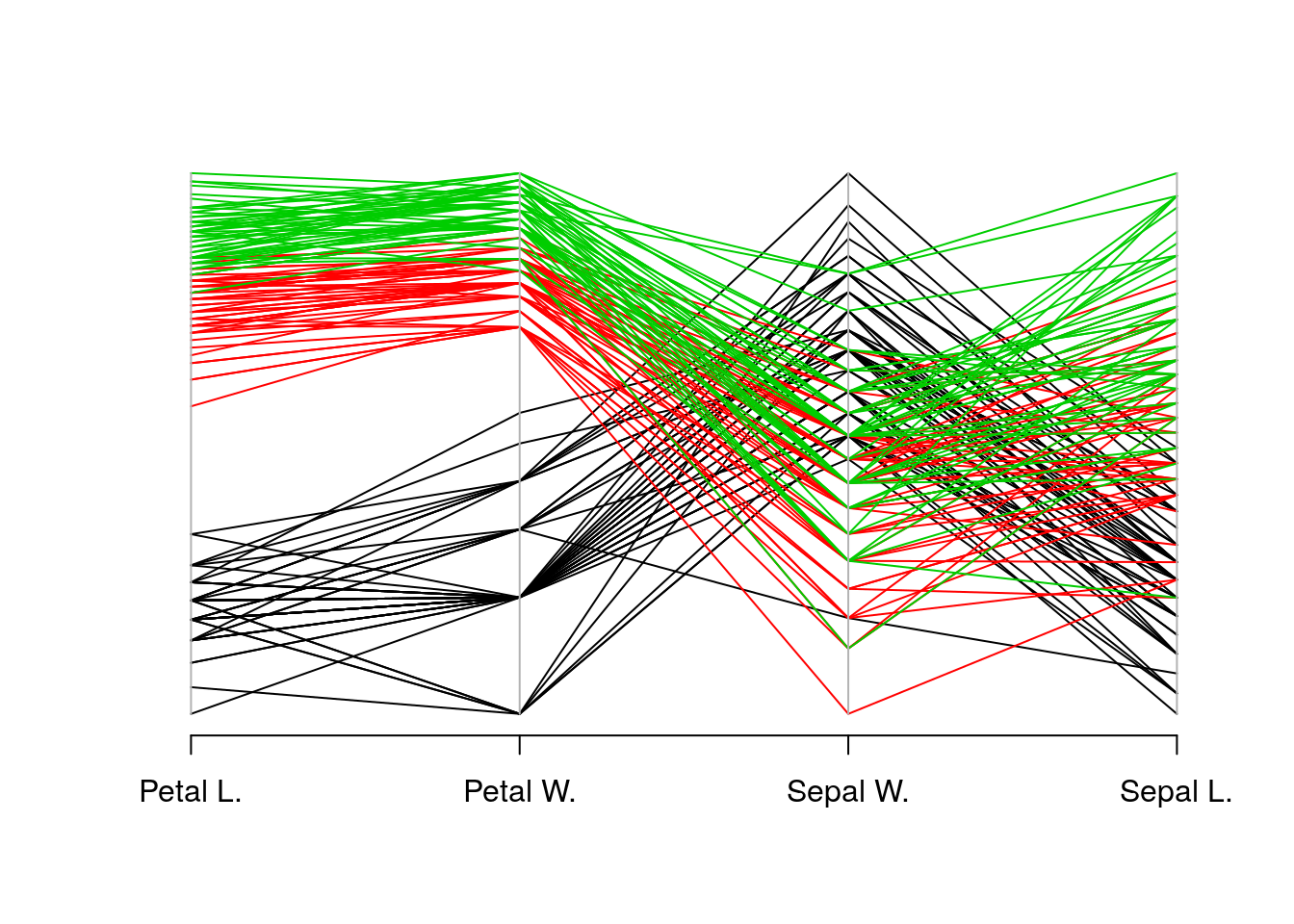

5.3 Mixed Type Data

Most real data sets will be of mixed type: both categorical and continuous. One approach to view such data, is to visualize the continuous variables separately, for each level of the categorical variables. There are, however, interesting dedicated visualization for such data.

5.3.1 Alluvial Diagram

An Alluvial plot is a type of Parallel Coordinate Plot for multivariate categorical data. It is particularly interesting when the \(x\) axis is a discretized time variable, and it is used to visualize flow.

The following example, from the ggalluvial package Vignette by Jason Cory Brunson, demonstrates the flow of students between different majors, as semesters evolve.

library(ggalluvial)
data(majors)
majors$curriculum <- as.factor(majors$curriculum)
ggplot(majors,
       aes(x = semester, stratum = curriculum, alluvium = student,
           fill = curriculum, label = curriculum)) +
  scale_fill_brewer(type = "qual", palette = "Set2") +
  geom_flow(stat = "alluvium", lode.guidance = "rightleft",
            color = "darkgray") +
  geom_stratum() +
  theme(legend.position = "bottom") +
  ggtitle("student curricula across several semesters")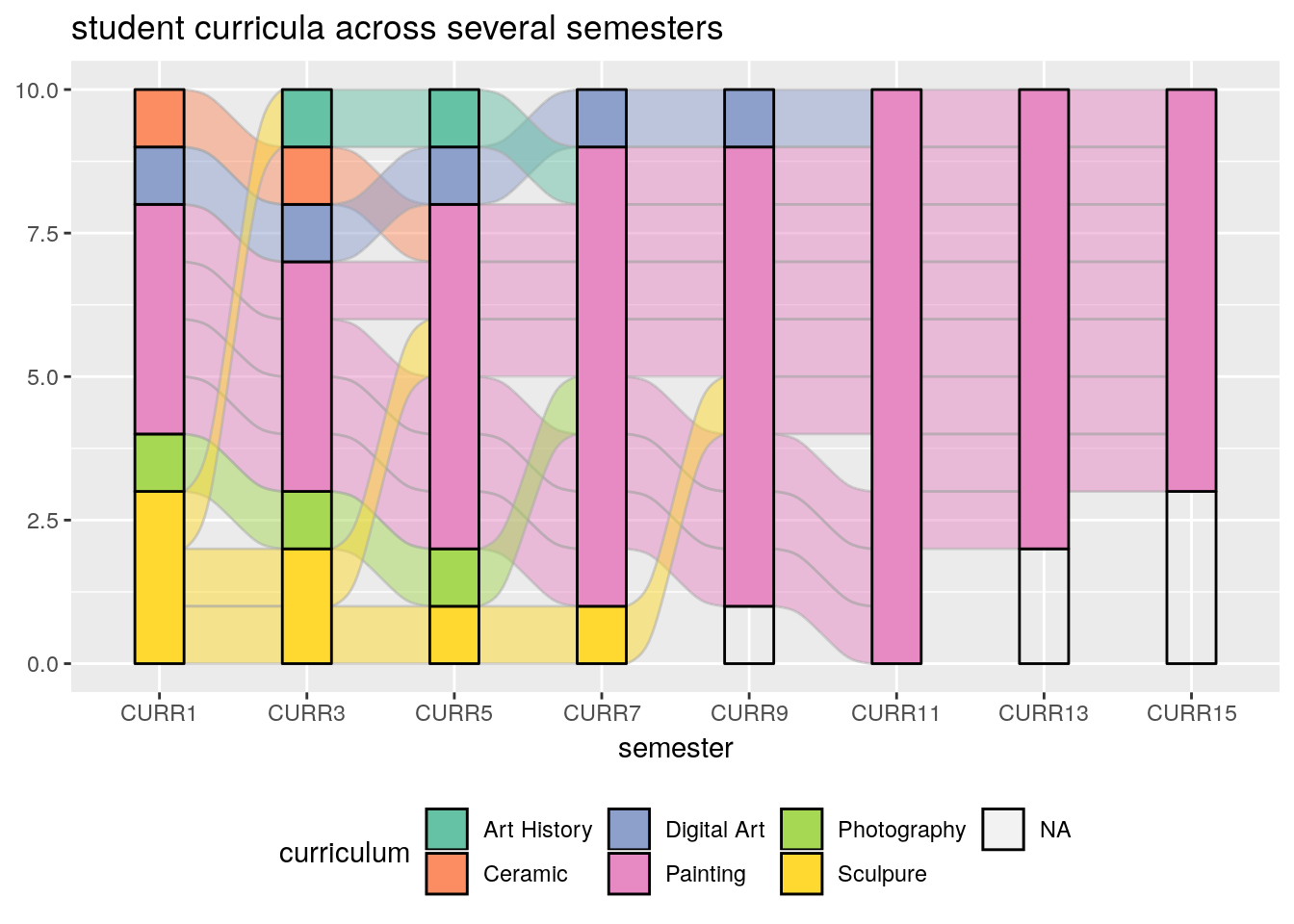

Things to note:

  • We used the ggalluvial package of the ggplot2 ecosystem. More on ggplot2 in the Plotting Chapter.
  • Time is on the \(x\) axis. Categories are color coded.
Remark. If the width of the lines encode magnitude, the plot is also called a Sankey diagram.

5.4 Bibliographic Notes

Like any other topic in this book, you can consult Venables and Ripley (2013). The seminal book on EDA, written long before R was around, is Tukey (1977). For an excellent text on robust statistics see Wilcox (2011).

5.5 Practice Yourself

  1. Read about the Titanic data set using ?Titanic. Inspect it with the table and with the ftable commands. Which do you prefer?

  2. Inspect the Titanic data with a plot. Start with plot(Titanic) Try also lattice::dotplot. Which is the passenger category with most survivors? Which plot do you prefer? Which scales better to more categories?

  3. Read about the women data using ?women.
    1. Compute the average of each variable. What is the average of the heights?
    2. Plot a histogram of the heights. Add ticks using rug.
    3. Plot a boxplot of the weights.
    4. Plot the heights and weights using a scatter plot. Add ticks using rug.

  4. Choose \(\alpha\) to define a new symmetry measure: \(1/2(x_\alpha+x_{1-\alpha})-x_{0.5}\). Write a function that computes it, and apply it on women’s heights data.

  5. Compute the covariance matrix of women’s heights and weights. Compute the correlation matrix. View the correlation matrix as an image using lattice::levelplot.

  6. Pick a dataset with two LONG continous variables from ?datasets. Plot it using hexbin::hexbin.

References

Tukey, John W. 1977. Exploratory Data Analysis. Reading, Mass.

Venables, William N, and Brian D Ripley. 2013. Modern Applied Statistics with S-Plus. Springer Science & Business Media.

Wilcox, Rand R. 2011. Introduction to Robust Estimation and Hypothesis Testing. Academic Press.